오늘은 정규분포 그래프를 matplotlib을 사용하여 시각화해보겠습니다.
정규분포의 사전적 정의는 다음과 같습니다.
도수(度數) 분포 곡선이 평균값을 중앙으로 하여 좌우 대칭으로 종 모양을 이루는 분포.
정규분포의 평균값에는 많은 데이터가 모여있기 때문에 다른 값들보다 높고 정규분포가 퍼진 정도는 표준편차에 의해 결정됩니다.
표준정규분포는 평균이 0이고 표준편차가 1인 정규분포입니다.
그럼 이제 정규분포 그래프를 시각화해보도록 합시다.
확률밀도함수
정규분포 그래프는 확률밀도함수에 의해 그려집니다.
확률밀도함수란 특정한 값의 확률을 나타내기 위한 함수입니다.
확률밀도함수를 통해 정규분포 그래프를 그릴 수 있습니다.
확률밀도함수는 다음과 같습니다.
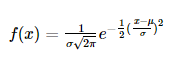
하지만 정규분포 곡선을 그리기 위해 항상 위의 식을 대입해야 하는 것은 아닙니다.
파이썬의 "scipy"라는 라이브러리에 확률 밀도 함수를 자동으로 계산해주는 기능이 있습니다.
import matplotlib.pyplot as plt #1
import numpy as np #2
from scipy.stats import norm #3
x = np.arange(0, 20, 0.001) #4
plt.figure(figsize=(15,10)) #5
plt.title('Normal Distribution') #6
plt.xlabel('x') #7
plt.ylabel('f(x)') #8
plt.grid() #9
plt.plot(x, norm.pdf(x, loc=10, scale=2)) #10
plt.show() #11- 그래프를 그리도록 도와주는 "matplotlib" 라이브러리의 모듈을 가져옵니다.
- 보통 행렬 관련 계산을 도와주는 "numpy" 모듈을 가져옵니다.
- 여러 가지 수학적 계산을 도와주는 "scipy" 라이브러리의 모듈을 가져옵니다.
- 0부터 20 이전까지의 수를 0.001 단위로 쪼개어서 array배열 형식으로 저장합니다.
- 그래프의 사이즈를 가로 15인치, 세로 10인치로 설정합니다.
- 제목을 "Normal Distribution"으로 설정합니다.
- x축 이름을 "x"로 지정합니다.
- y축 이름을 "f(x)"로 지정합니다.
- 그래프에 격자무늬를 넣습니다.
- x축에는 아까 만들었던 "x"변수를, y축에는 x를 평균(loc)이 10이고 표준편차(scale)가 2인 확률밀도함수로 계산한 값을 넣습니다.
- 그래프를 출력합니다.
출력 결과는 다음과 같습니다.

확률밀도함수를 직접 계산하지 않고 "norm"모듈의 "pdf"함수를 사용하여 그래프를 만들어 보았습니다.
"pdf"는 "probability density function"의 약자로 확률밀도함수를 의미합니다.
표준정규분포는 평균이 0이고 표준편차가 1인 정규분포이기 때문에 또한 위와 같은 방식으로 만들 수 있습니다.
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
x = np.arange(-4, 4, 0.001)
plt.figure(figsize=(15,10))
plt.title('Standard Normal Distribution')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.plot(x, norm.pdf(x, loc=0, scale=1))
plt.show()"pdf"함수의 평균(loc)에는 0을, 표준편차(scale)에는 1을 넣어주기만 하면 됩니다.
그래프의 대칭성을 보이기 위해 x의 배열은 -4부터 4 이전까지로 지정했습니다.
표준정규분포이기 때문에 그래프의 이름 앞에 "Standard"를 붙여주었습니다.
출력 결과는 다음과 같습니다.

평균이 0이기 때문에 0을 중심으로 대칭인 모습입니다.
표준편차가 이전보다 작아졌기 때문에 좀 더 완만한 모양을 보이는 것을 알 수 있습니다.
누적분포함수
누적분포함수는 특정한 구간의 확률을 나타내는 함수입니다.
정규분포 그래프를 적분하여서 구할 수 있습니다.
누적분포함수 또한 "scipy" 라이브러리를 사용하여 구할 수 있습니다.
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
x = np.arange(-4, 4, 0.001)
plt.plot(x, norm.pdf(x, loc=0, scale=1))
plt.title("Standard Normal Distribution")
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
cum = np.arange(-1, 1, 0.01) #1
plt.fill_between(cum, norm.pdf(cum), alpha=0.5, color='g') #2
pro = norm(0, 1).cdf(1) - norm(0, 1).cdf(-1) #3
plt.text(0, 0.02, round(pro,2), fontsize=20) #4
plt.show()- 확률 값을 구할 특정 구간의 범위를 설정합니다. -1부터 1 이전까지의 범위를 구해봅시다.
- 누적분포함수 값을 그래프에 나타내기 위해 특정 구간의 표준정규분포곡선 아래 영역에 색을 채워 넣습니다. alpha값은 투명도를 나타내고 0부터 1까지의 값을 넣을 수 있으며 1에 가까울수록 투명도가 낮습니다. 색깔은 초록색으로 설정합니다.
- -1과 1 사이의 누적분포함수 값을 구하기 위해 평균이 0이고 표준편차가 1인 그래프에서 1까지의 누적분포함수 값에서 -1까지의 누적분포함수 값을 빼줍니다.
- 그래프의 x축 0, y축 0.02의 위치에 -1과 1사이의 누적분포함수 값에서 소수점 2의 자리까지 반올림한 값을 사이즈 20의 크기로 넣습니다.
출력 결과는 다음과 같습니다.

누적분포함수값을 "norm" 모듈의 "cdf" 함수를 사용하여 계산하였습니다.
"cdf"는 "cumulative distribution function"의 약자로 누적분포함수를 의미합니다.
-1과 1 사이의 확률 값은 그래프에 초록색으로 나타낸 부분의 넓이이고 그 넓이는 0.68입니다.
표준정규분포에서 랜덤한 한 데이터를 추출할 때 -1과 1 사이의 값일 확률이 약 68%라는 뜻입니다.
참고로 -2부터 2까지의 구간에 속한 누적분포함수 값은 약 0.95이고, -3부터 3까지의 구간에 속한 누적분포함수 값은 약 0.997입니다.
오늘은 matplotlib을 사용하여 정규분포 그래프를 그려보았습니다.
직접 실행해 볼 수 있도록 밑에 코랩 링크 남겨놓습니다.
https://colab.research.google.com/drive/1-OfbwWtq4s_FKDVVWfGwakrPZkaSE2go?usp=sharing
정규분포 그래프 시각화(배포용).ipynb
Colaboratory notebook
colab.research.google.com
'프로젝트 > 시각화' 카테고리의 다른 글
| [Python] 우리나라 GDP와 GNP의 차이에 대한 분석 (0) | 2022.05.06 |
|---|---|
| [Python] 우리나라의 GDP와 GNP의 연도별 변화추세 (0) | 2022.05.05 |
| [Python] 몬테카를로 방법을 이용하여 원주율, 파이(π)값 구하기 (0) | 2022.03.19 |
| [Python] (3)올웨더 기반 효율적 투자선 구현 : 시각화 (0) | 2022.03.06 |
| [Python] 시각화를 통해 가격대가 다른 두 주식 비교하기 (4) | 2022.02.19 |



