[Python] 통화량에 따른 물가의 변화 선형회귀 분석

화폐수량설에 따르면 통화량 변화는 물가에 영향을 미치고 통화량 증가율과 물가상승률은 1대 1 관계를 가집니다.

 

그렇다면 현실세계에서도 화폐수량설 이론과 같은 결과가 나올까요?

 

오늘은 우리나라의 통화량 지표(M2)와 물가 지표(GDP 디플레이터)를 가지고 둘의 선형 관계를 분석해보겠습니다.

 

코드에 대한 자세한 설명은 생략했습니다. 자세한 설명을 보고 싶으시면 이전 포스팅을 참고해주세요.

https://bigdata-doctrine.tistory.com/20

[Python] 우리나라의 GDP와 GNP의 연도별 변화추세

 

 

데이터 수집

---

https://ecos.bok.or.kr/

한국은행경제통계시스템

ecos 사이트에서 M2(광의통화, 말잔), GDP 디플레이터, GDP 디플레이터 등락률 데이터 자료를 csv형식으로 받습니다.

 

1960년부터 2021년까지의 데이터를 가져옵니다.

 

csv파일에 들어가서 필요없는 데이터는 모두 지워주고 필요한 데이터만 남겨줍니다.

이런식으로 정리하면 됩니다

 

 

데이터프레임 생성

---

import pandas as pd

# csv파일 데이터프레임 형식으로 변환
df = pd.read_csv("ECOS_TABLE_20220521_094437.csv", encoding="CP949")

# 데이터프레임 행열 변환
df1 = df.transpose() 
df1.rename(columns=df1.iloc[0], inplace=True) 
df1.drop(df1.index[0], inplace=True)

# 데이터프레임 열 이름 영어로 변환
df2 = df1.rename(columns={"M2(광의통화, 말잔)": "M2", "GDP 디플레이터": "GDP_deflator",
                          "  (등락률)": "GDPd_growth"})

df2

행열이 변환되고 열 이름을 영어로 바꾼 df

수집한 csv파일을 읽고 데이터프레임 형식으로 변환합니다.

 

연도가 열에 있는 읽기 어려운 형식으로 되어 있기 때문에 행열을 바꾸어줍니다.

 

시각화할 때 한글이 깨져 보이므로 한글로 된 열 이름을 영어로 바꾸어줍니다.

 

 

데이터 숫자 변환 & M2 증가율 생성

---

# 개별 데이터 숫자 변환
for i in df2.index:
    for c in df2.columns:
        if type(df2[c][i]) == str:
            rm = df2[c][i].replace(",","")
            df2[c][i] = float(rm)

# 전체 데이터 숫자 변환
for c in df2.columns:
    df2[c] = df2[c].astype(float)

# M2 증가율 데이터 생성
df3 = df2.copy()
df3["M2_growth"] = df3["M2"].pct_change(1) * 100

df3

숫자 변환 & M2 증가율을 반영한 df

ecos에서 수집한 데이터는 1000이하의 데이터는 float형이고 1000 이상의 데이터는 str형 이런 식으로 자료형이 섞여 있어서 astype으로 전체 데이터를 숫자로 변환하려면 오류가 생깁니다.

 

개별데이터를 먼저 숫자형으로 변환해주고 그다음에 전체 데이터를 숫자형으로 변환해줍니다.

 

숫자형으로 변환하는데 성공했다면 이제 M2 증가율을 계산할 수 있겠죠?

 

pct_change 함수를 사용하여 M2 증가율을 계산해주고 새로운 데이터프레임 열에 넣어줍니다.

 

 

통화량 & 물가 산포도 시각화

---

import matplotlib.pyplot as plt

df3.plot.scatter(x="M2", y="GDP_deflator", figsize=(12,8), s=50)
plt.title("Korea M2 & GDP deflator regression analysis", size=20)
plt.show()

통화량과 물가의 산포도

x축에 M2를 놓고 y축에 GDP 디플레이터를 넣어 산포도를 만들어보았습니다.

 

뭔가 유의미한 상관관계를 보이는 것처럼 보이나 선형관계가 아니군요.

 

선형 회귀분석을 하기 위해서는 두 데이터가 선형관계를 보여야 하므로 두 지표에 자연로그 값을 취하여 선형 그래프로 만들어줍니다. 

 

import numpy as np

df4 = df3.copy()
df4["ln_M2"] = df4["M2"].apply(lambda x: np.log(x))
df4["ln_GDPd"] = df4["GDP_deflator"].apply(lambda x: np.log(x))

df4

M2와 GDP 디플레이터에 자연로그를 취한 값을 새로운 열에 추가한 df

apply 함수와 lambda 함수를 사용하여 간단하게 자연로그를 취한 값을 새로운 열에 추가해줍니다.

 

이제 ln M2와 ln GDP 디플레이터의 산포도를 구해봅시다.

df4.plot.scatter(x="ln_M2", y="ln_GDPd", figsize=(12,8), s=50)
plt.title("Korea ln M2 & ln GDP deflator regression analysis", size=20)
plt.show()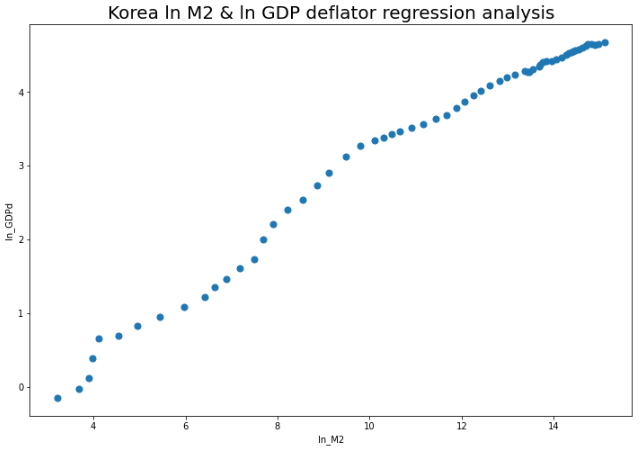

ln M2와 ln GDP 디플레이터의 산포도

두 지표에 자연로그 값을 취하니 일정한 선형관계가 만들어진 것을 확인할 수 있습니다.

 

선형 회귀분석을 하기에 좋은 형식으로 나왔네요.

 

 

통화량 & 물가 회귀분석

---

from statsmodels.formula.api import ols

model = ols("ln_GDPd ~ ln_M2", data=df4).fit()

회귀분석을 하기 위해 statsmodels 모듈을 가져옵니다.

 

ols 함수 안의 따옴표 안에 "종속변수 ~ 독립변수" 형식으로 넣어줍니다.

 

우리는 통화량(M2)이 물가(GDP 디플레이터)에 주는 영향을 분석하고 있으므로 독립변수에 ln M2를 종속변수에 ln GDP 디플레이터를 넣어줍니다.

 

print(model.summary())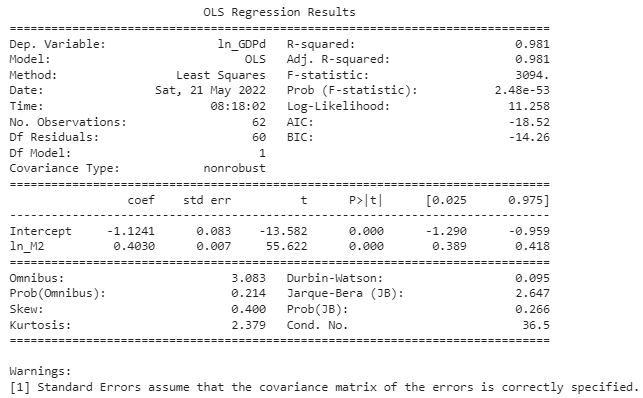

모델 개요

R-squared 값이 0.981로 매우 높은 수치를 보이고있습니다.

 

R-squared 값은 0과 1 사이에 위치하며 주어진 회귀분석 모델이 두 지표의 관계를 얼마나 잘 설명해주는 지를 나타냅니다. 1에 가까울수록 높은 설명력을 나타냅니다.

 

나중에 보겠지만 실제로 관측된 값이 선형회귀선과 가까운 경우 R-squared 값이 높습니다.

 

Intercept의 coef는 선형회귀선의 y-절편이고 ln_M2의 coef는 선형회귀선의 기울기입니다.

 

선형 회귀분석 결과에 따르면 ln_M2의 값이 0일 때 ln_GDP 디플레이터 값은 약 -1.12입니다.

 

두 지표에 자연로그를 취해주었으므로 ln_M2의 coef값인 0.4030은 통화량이 1% 증가할 때, 물가가 약 0.4% 증가함을 나타냅니다.

 

P값이 0이기 때문에 5% 유의 수준에서 귀무가설이 기각됩니다. 우연에 의한 결과가 아님을 나타냅니다.

 

이제 회귀분석에 의한 예측값을 구해봅시다.

intercept = model.params[0]
coef = model.params[1]

df5 = df4.copy()
df5["predict"] = intercept + df5["ln_M2"] * coef 
df5 = df5[["ln_M2", "ln_GDPd", "predict"]]

df5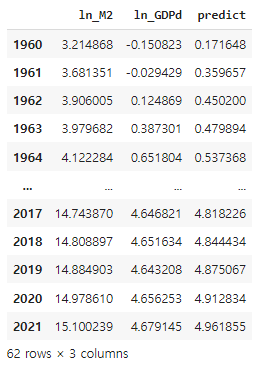

예측값이 포함된 데이터프레임

intercept 변수에 -1.1241을 coef 변수에 0.4030을 넣습니다.

 

데이터프레임에 predict라는 이름의 새로운 열을 만들고 선형회귀 함수를 넣어줍니다.

(y=ax+b ; a에 기울기 값을, b에 절편 값을 넣어줍니다)

 

predict열에는 ln_M2에 따른 ln_GDP 디플레이터의 예측값이 생성됩니다. (회귀분석에 따른)

 

이제 회귀분석선을 시각화해봅시다.

plt.figure(figsize=(12, 8))
plt.plot(df5["ln_M2"], df5["predict"], c="r", label="Linear regression")
plt.scatter(df5["ln_M2"], df5["ln_GDPd"])
plt.title("Korea ln M2 & ln GDP deflator regression analysis", size=20)
plt.xlabel("ln_M2")
plt.ylabel("ln_GDPd")
plt.legend(fontsize=12)
plt.show()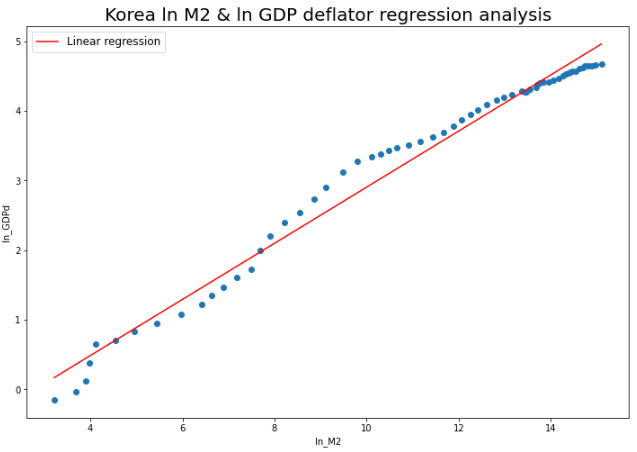

ln M2와 ln GDP의 선형회귀선

두 지표의 선형회귀선을 시각화해보았습니다.

 

이전에 R-squared값이 높았던 이유는 선형회귀선 근처에 실제 관측값이 많이 위치해있기 때문입니다.

 

 

통화량 증가율 & 물가상승률 회귀분석

---

이제 통화량 증가율과 물가상승률 데이터로 회귀분석을 해봅니다.

# 자연로그값으로 변환
df7 = df5.copy()
df7["ln_M2g"] = df7["M2_growth"].apply(lambda x: np.log(x))
df7["ln_GDPdg"] = df7["GDPd_growth"].apply(lambda x: np.log(x))

# 회귀분석 모델 생성
model2 = ols("ln_GDPdg ~ ln_M2g", data=df7).fit()
intercept2 = model2.params[0]
coef2 = model2.params[1]

# 예측값 생성
df7["predict"] = intercept2 + df7["ln_M2g"] * coef2
df7 = df7[["ln_M2g", "ln_GDPdg", "predict"]]

df7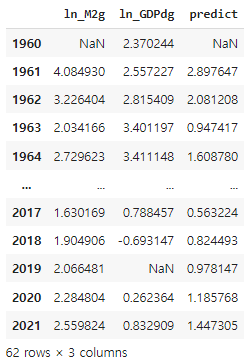

통화량증가율, 물가상승률, 예측값

 

print(model2.summary())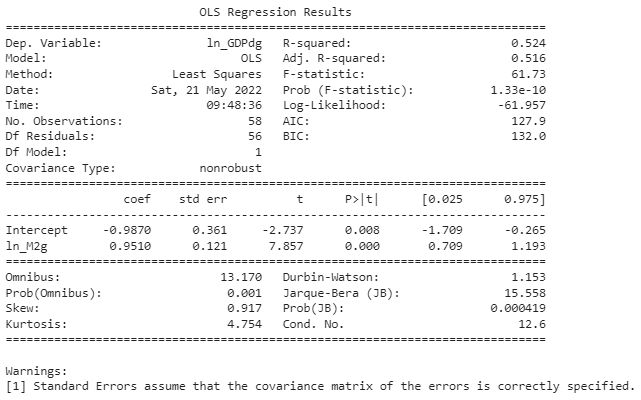

모델 개요

 

plt.figure(figsize=(12, 8))
plt.plot(df7["ln_M2g"], df7["predict"], c="r", label="Linear regression")
plt.scatter(df7["ln_M2g"], df7["ln_GDPdg"])
plt.title("Korea ln M2 growth & ln GDP deflator growth regression analysis", size=20)
plt.xlabel("ln M2 growth(%)")
plt.ylabel("ln GDPd growth(%)")
plt.legend(fontsize=12)
plt.show()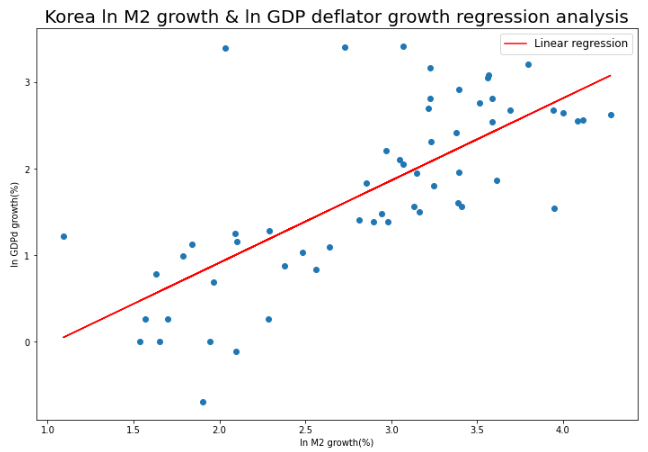

ln_M2증가율과 ln_GDP디플레이터 증가율의 회귀분석선

 

R-squared값이 0.524로 이전의 회귀분석 모델보다 설명력이 떨어지는 것을 확인할 수 있습니다. 그래도 이 정도면 두 지표 간의 관계를 충분히 잘 설명하는 것으로 보입니다.

 

두 지표의 성장률을 이용하여 구했으므로 기울기 값인 0.9510은 통화량 증가율이 1%(1%p 아닙니다)증가할 때 물가상승률이 약 0.95% 증가한다는 것을 확인할 수 있습니다. 

 

p값이 0.05보다 작기 때문에 5% 유의 수준에서 귀무가설을 기각합니다.

 

원래 자연로그에는 음수 값을 넣을 수 없습니다. (음수 값을 취할 경우 None데이터가 생성됩니다)

 

따라서 이 모델은 통화량 증가율이나 물가상승률이 마이너스인 경우는 설명해주지 못합니다.

 

하지만 통화량 증가율과 물가상승률은 음수 값이 많지 않기 때문에 모델 자체는 유의미하다고 할 수 있을 것 같습니다.

 

 

---

우리나라의 통화량 지표(M2)와 물가 지표(GDP 디플레이터)를 가지고 둘의 선형 관계를 분석해보았습니다.

 

통화량과 물가 두 지표 사이에는 강한 상관관계가 존재하는 것을 확인할 수 있었습니다.

 

밑의 링크에서 실습해보실 수 있습니다.

https://colab.research.google.com/drive/1CpXTp2A8lQuG2f72uts5PlR3CQy7nmXC?usp=sharing 

통화량에 따른 물가의 변화 선형회귀 분석(배포용).ipynb