[Python] 리스크 변화에 따른 수익률 변화 회귀 분석

오늘은 올웨더 포트폴리오 종목인 주식, 중기채, 장기채, 금, 원자재의 5가지 etf로 구성된 효율적 투자선을 통해 리스크 변화에 따른 수익률의 변화를 회귀분석으로 분석해보겠습니다.

 

이전 포스팅에서 이미 효율적 투자선을 시각화하고 분석해보았기 때문에 이전에 썼던 코드를 그대로 가져왔습니다.

 

효율적 투자선을 시각화하는 프로젝트는 밑의 포스팅을 참고하시길 바랍니다.

https://bigdata-doctrine.tistory.com/12

[Python] (3)올웨더 기반 효율적 투자선 구현 : 시각화

 

 

효율적 투자선 추출

---

이전 시간에는 효율적 투자선만 따로 추출하지 않고 산포도 상에서 효율적 투자선이 어디인지 살펴보기만 했습니다.

 

하지만 이번에는 회귀분석을 하기 위해 효율적 투자선 부분의 데이터가 필요하기 때문에 따로 추출하는 작업을 해줍니다.

 

각각의 리스크별로 최대의 수익률을 가지는 포트폴리오를 추출해보겠습니다.

 

세트 자료형을 사용하는 이유는 중복을 허용하지 않는 세트의 특성 때문입니다.

 

각각의 리스크가 중복이 되면 안 되므로 세트를 사용해줍니다. 

# 리스크 세트 생성
rsk_set = set()
round = 3
for r in port_df["Risk"]:  # 1
    rsk = np.round(r, round)
    rsk_set.add(rsk)

# 리스크 반올림
port_df["Risk2"] = port_df["Risk"].apply(lambda x: np.round(x, round))  # 2

# 리스크, 최대 수익률 딕셔너리 생성
ret_lst = []
dic = {}
for rsk in rsk_set:  # 3
    ret_lst = []
    row = port_df[port_df["Risk2"] == rsk]
    for ret in row["Returns"]:  # 4
        ret_lst.append(ret)
    max_ret = max(ret_lst)  # 5
    dic[rsk] = max_ret

1. port_df 데이터프레임의 Risk 열의 데이터를 소수점 셋째 자리까지 반올림하여 rsk_set에 넣어줍니다. set 자료형은 중복을 허용하지 않으므로 세트 안의 숫자는 모두 다른 숫자입니다.
2. port_df에 Risk2 열을 만들어 Risk 열을 3째자리까지 반올림한 값을 넣어줍니다. 이는 후에 각 리스크 별 수익률을 구하기 위함입니다.
3. rsk_set에서 각각의 리스크를 for문을 활용해 내보내 줍니다. 데이터프레임 행 중 port_df["Risk"]와 rsk가 같은 행들을 모두 row변수에 저장합니다. row변수는 port_df["Risk"]와 rsk가 같은 행들은 모아놓은 데이터프레임입니다.
4.  row 데이터프레임에서 Returns열을 추출하여 ret_lst 리스트에 저장합니다. 이 리스트는 port_df["Risk"]와 rsk가 같은 특정한 리스크 상태에서의 수익률 데이터를 담고 있습니다.
5. ret_lst에서 최댓값을 추출하여 max_ret변수에 저장합니다. 각 리스크 별 최대 수익률이 max_ret 변수에 저장됩니다. 이는 key는 리스크, value는 수익률 최댓값을 나타내는 딕셔너리에 저장합니다.

dic

밑에 수많은 데이터가 있다

각 리스크별 최대 수익률을 추출해내었다.

 

 

선형 회귀선 시각화

---

plt.figure(figsize=(12, 8))  
plt.scatter(x=list(dic.keys()), y=list(dic.values()), s=10)
plt.title("Efficient Frontier", size=20)
plt.xlabel("Risk")
plt.ylabel("Returns")
plt.grid()
plt.show()

x축에는 dic의 key인 리스크를, y축에는 dic의 value인 각 리스크별 수익률 최댓값을 넣습니다.

 

효율적 투자선

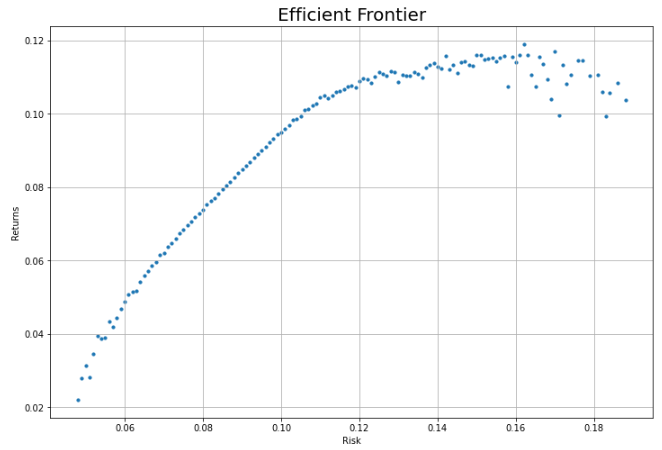
효율적 투자선을 따로 추출하여 시각화하는 데 성공했습니다.

 

이제 이것을 가지고 회귀분석 모델을 만든 후 회귀선을 시각화해보도록 하겠습니다.

 

from statsmodels.formula.api import ols  # 1

df = pd.DataFrame({"Risk": list(dic.keys()), "Returns": list(dic.values())})  # 2
model = ols("Returns ~ Risk", data=df).fit()  # 3
intercept = model.params[0]  # 4
coef = model.params[1]  # 5

df["predict"] = intercept + df["Risk"] * coef  # 6
df = df[["Risk", "Returns", "predict"]] 

plt.figure(figsize=(15, 10))
plt.plot(df["Risk"], df["predict"], c="r", label="Linear regression")  # 7
plt.title("Efficient Frontier", size=20)
plt.grid()
plt.xlabel("Risk")
plt.ylabel("Returns")
plt.legend(fontsize=15)
plt.scatter(df["Risk"], df["Returns"], s=10)
plt.show()

1. 회귀분석 모델을 생성하기 위해 statsmodels 모듈을 가져옵니다.
2. 회귀분석을 진행하기 위해 Risk와 Returns를 데이터프레임에 저장합니다.
3. Risk가 독립변수, Returns가 종속변수인 모델을 만듭니다.
4. 절편 값을 intercept 변수에 넣어줍니다.
5. 계수 값을 coef 변수에 넣어줍니다.
6. 절편과 계수를 사용해 회귀식을 만들어 예측값을 계산합니다. 그 후 predict 열에 넣어줍니다.
7. 가로축에 리스크, 세로축에 예측값을 가지는 회귀선을 생성합니다.

회귀선이 효율적 투자선을 잘 설명해주지 못하는 듯 하다

그래프를 도출해내 보았지만 회귀선이 효율적 투자선을 잘 설명해주지 못하는 듯합니다.

 

그 이유는 현재의 효율적 투자선이 선형 관계가 아니기 때문입니다.

 

리스크가 0.11 미만인 지점(11% 미만)에서는 선형 관계를 가지는 것으로 보이므로 그 부분만 따로 추출하여 회귀분석을 진행해보겠습니다.

 

 

리스크가 11% 미만인 수준에서의 회귀선 시각화

---

# 위험률이 11% 미만인 수준에서 회귀분석 실행
df1 = df[df["Risk"] < 0.11]
model1 = ols("Returns ~ Risk", data=df1).fit()
intercept1 = model1.params[0]
coef1 = model1.params[1]

df1["predict"] = intercept1 + df1["Risk"] * coef1
df1 = df1[["Risk", "Returns", "predict"]]

plt.figure(figsize=(15, 10))
plt.plot(df1["Risk"], df1["predict"], c="r", label="Linear regression")
plt.title("Efficient Frontier", size=20)
plt.grid()
plt.xlabel("Risk")
plt.ylabel("Returns")
plt.legend(fontsize=15)
plt.scatter(df1["Risk"], df1["Returns"], s=10)
plt.show()

리스크와 수익률의 관계를 잘 설명하는 회귀선

데이터프레임에서 리스크가 0.11 미만인 지점을 따로 추출하여 회귀분석을 진행해보았습니다.

 

회귀선과 관측값들의 잔차가 크지 않은 것으로 보아 회귀선이 리스크와 수익률 간의 관계를 잘 설명해주는 듯 보입니다.

 

 

회귀분석 요약

---

print(model1.summary())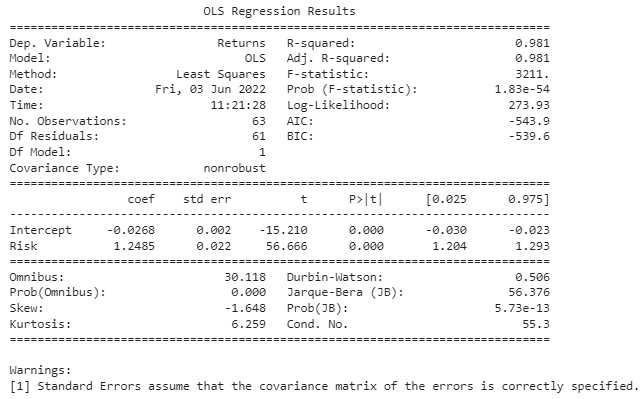

회귀분석 요약

R-squared 값이 0.981로 1과 매우 가까운 것을 보아 회귀 모델에서 독립변수가 종속변수를 아주 잘 설명해주는 것을 알 수 있습니다.

 

p-값이 0이므로 5% 유의 수준에서 귀무가설을 기각합니다. 둘의 관계가 우연에 의한 것이 아님을 의미합니다.

 

계수 값이 약 1.2로 리스크를 1%p 증가시키면 수익률이 약 1.2%p 증가한다는 것을 알 수 있습니다.

 

 

리스크가 11% 이상인 수준에서의 회귀분석

---

그렇다면 과연 리스크가 11% 이상인 수준에서도 리스크와 수익률은 유의미한 관계를 나타낼까요?

 

회귀분석을 통해 알아보겠습니다.

df2 = df[df["Risk"] >= 0.11]
model2 = ols("Returns ~ Risk", data=df2).fit()
intercept2 = model2.params[0]
coef2 = model2.params[1]

df2["predict"] = intercept2 + df2["Risk"] * coef2 
df2 = df2[["Risk", "Returns", "predict"]]

plt.figure(figsize=(15, 10))
plt.plot(df2["Risk"], df2["predict"], c="r", label="Linear regression")
plt.title("Efficient Frontier", size=20)
plt.grid()
plt.xlabel("Risk")
plt.ylabel("Returns")
plt.legend(fontsize=15)
plt.scatter(df2["Risk"], df2["Returns"], s=10)
plt.show()

리스크가 11% 이상인 수준에서는 회귀선이 둘의 관계를 잘 설명해주지 못한다

리스크가 11% 이상인 수준에서는 리스크와 수익률 간의 관계가 유의미하지 않은 것처럼 보입니다.

 

회귀분석 요약을 통해 알아보겠습니다.

print(model2.summary())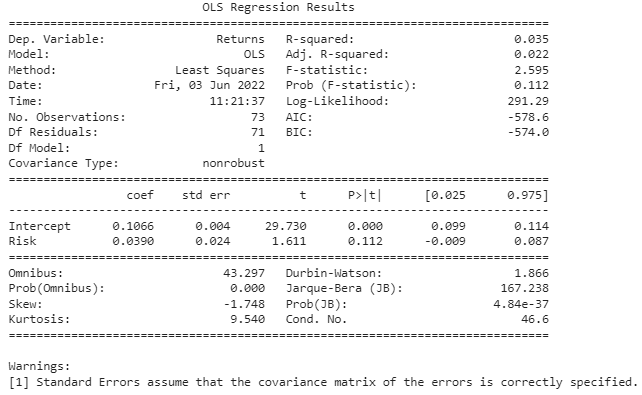

리스크가 11% 이상인 지점에서의 회귀분석 요약

R-squared 값이 0.035로 매우 낮아 회귀분석이 둘의 관계를 잘 설명해주지 못한다는 것을 알 수 있습니다.

 

p-값은 0.112로 5% 유의 수준에서 대립 가설을 기각합니다. 둘의 관계가 우연에 의한 것일 수 있음을 의미합니다.

 

유의미한 결과를 도출해내지 못할 것으로 보이므로 계수 값에 대해서는 이야기하지 않도록 하겠습니다.

 

 

결론

---

이번 프로젝트를 통해서 도출해낸 인사이트는 무엇일까요?

 

위험률이 11% 미만인 경우 위험률을 1%p 증가시키면  수익률을 약 1.2%p 증가시킬 수 있습니다.

 

그리고 위험률이 11% 이상인 경우는 위험률과 수익률 간의 상관관계가 매우 낮았습니다.

 

그렇다는 것은 위험률을 11%까지 증가시키면 위험률 대비 수익률을 극대화시킬 수 있다는 것입니다.

 

위험률 대비 수익률을 나타내는 지표가 바로 샤프지수입니다.

 

실제 이전에 구한 효율적 투자선 내에서의 샤프지수 최댓값을 보이는 지점이 10%~11% 사이에 있는 것을 확인할 수 있습니다.

별 표시된 지점이 샤프지수 최댓값을 보이는 포트폴리오

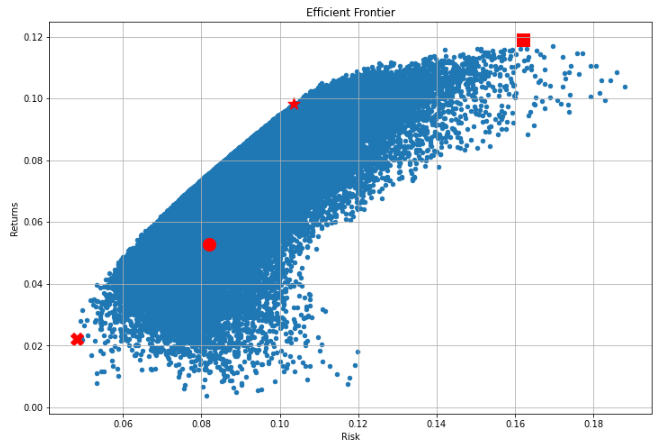
10%와 11% 사이에 있는 이유는 이전에 구한 리스크 11% 미만인 지점에서의 회귀선을 보면 위험률 10% 이후로 위험률 증가율 대비 수익률 증가율이 감소하기 때문입니다.

 

 

---

오늘은 올웨더 포트폴리오 종목인 주식, 중기채, 장기채, 금, 원자재의 5가지 etf로 구성된 효율적 투자선을 통해 리스크 변화에 따른 수익률의 변화를 회귀분석으로 분석해보았습니다.

 

이번 프로젝트를 통해 얻은 인사이트는

1. 리스크가 11% 미만인 지점에서의 리스크와 수익률 간의 관계는 유의미하다.
2. 그 지점에서 리스크를 1%p 증가시키면 수익률은 약 1.2%p 증가한다.
3. 리스크가 11% 이상인 지점에서의 리스크와 수익률 간의 관계는 무의미하다.
4. 따라서 리스크를 약 11% 수준까지 끌어올릴 경우 샤프지수를 최대화할 수 있다.

등등이 있습니다.

 

주의할 점은 다음과 같습니다.

1. 미국 주식, 중기채, 장기채, 금, 원자재 5가지 종목의 포트폴리오를 통해 도출한 결론이다.
2. 시뮬레이션을 통해 도출된 결과이므로 실행 시마다 약간씩 달라질 수 있다.
3. 2016년 이후 데이터만을 사용했기 때문에 이전의 시장은 설명해주지 못한다.  
4. 과거의 데이터를 사용하여 분석했기 때문에 미래에도 같을지는 보장할 수 없다.

 

리스크를 1%p 증가시키면 수익률이 약 1.2%p 증가한다는 것은 진리가 아닙니다.

 

미래에 추가적으로 데이터가 쌓여 다시 분석을 해보면 다른 결과가 도출될 수 있습니다.

 

이번 프로젝트를 통해 도출한 모든 결과가 바뀔 수 있습니다.

 

밑에 코랩 링크 남겨놓으니 실습해보세요.

https://colab.research.google.com/drive/1Quo21U92oyxkzGq6GLNSpNVkCaR3Osd-?usp=sharing 

리스크 변화에 따른 수익률 변화 회귀분석(배포용).ipynb