단순 선형회귀는 X의 변화에 따른 Y의 평균적인 변화를 알아볼 수 있는 좋은 도구입니다.
하지만, 그전에 자료 값들이 특정한 조건들을 만족하는지를 살펴보아야 합니다.
특정한 조건들을 만족하지 않는 자료 값들로 회귀 분석을 할 경우 분석의 결과는 유용하지 않을 수 있습니다.
지금부터 계량경제학 내의 단순 선형회귀 모형에 관한 가정들에 대해 알아보겠습니다.
개요
먼저 개략적으로 살펴보겠습니다. 가정들은 SR1~SR6로 이루어져 있으며, SR은 "Simple Rregresion", 즉 단순 선형회귀를 의미합니다.
- SR1 : 계량경제 모형
- SR2 : 강 외생성
- SR3 : 조건부 동분산
- SR4 : 조건부적으로 상관되지 않은 오차
- SR5 : 설명변수는 변화해야만 한다
- SR6 : 오차 정규성(선택적)
하나하나 자세히 알아봅시다.
SR1 : 계량경제 모형
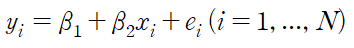
SR2 : 강 외생성
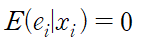
위의 조건이 만족할 경우 설명변수 x는 강하게 외생적, 즉 강 외생적이라고 합니다.
1. 무작위 오차항의 무조건부 기댓값 또한 0이 된다.

모든 x값에 대한 무작위 오차항의 조건부 평균이 0이기 때문에 무조건부 기댓값 또한 0이 됩니다.
2. 무작위 오차항과 그에 상응하는 관찰값 x의 공분산이 0이 된다.

x값으로 오차항을 예측할 수 없다는 것은 둘 사이의 상관관계가 0, 즉 공분산이 0이라는 말과 같습니다.
위의 조건이 만족할 경우 설명변수 x는 외생적이라고 합니다. 이 전에 말한 강 외생적이라는 표현보다 약한 표현입니다.
위의 두 성질 중 하나라도 참이 아니면 강 외생성 가정은 만족하지 않습니다.
강 외생성 가정이 만족할 경우 다음과 같은 회귀 함수를 도출할 수 있습니다.

위의 식은 x의 값이 주어졌을 때의 y의 (조건부) 평균을 나타내는 식입니다.
위의 식을 통해 x가 Δx만큼 변할 때, y의 (조건부) 평균값이 β2 x Δx만큼 변화한다고 말할 수 있습니다.

지금까지 계량경제학 내의 단순 선형회귀 모형에 관한 두 가지 가정들에 대해 알아보았습니다.
다음 시간에는 나머지 가정들을 살펴보는 시간을 갖도록 하겠습니다.
'정보 > 수리통계' 카테고리의 다른 글
| 회귀 모수에 대한 검정: 유의성검정과 p-값 (0) | 2023.08.22 |
|---|---|
| 회귀 모수에 대한 검정: 가설검정 (0) | 2023.07.29 |
| 회귀 모수 추정: 표준오차(se)를 통한 구간 추정 (2) | 2023.07.25 |
| 회귀 모수 추정: 최소제곱법(OLS) 활용 (0) | 2023.07.21 |
| 단순 선형회귀 모형에 관한 가정 (SR3~SR6) (0) | 2023.03.13 |

