오늘은 단순 선형회귀 모형의 회귀모수를 추정하는 방법을 알아보도록 하겠습니다.
회귀 모수를 찾는 대표적인 방법으로는 최소제곱법(OLS)이 있습니다.
최소제곱법은 통계적인 모수 추정 방법으로 추정량(공식)을 사용하여 추정값을 찾아내는 방식입니다.
오늘은 최소제곱법(OLS)에 대해 살펴보도록 하겠습니다.
회귀 모수란?
관측값 쌍들이 단순 선형회귀의 가정을 모두 만족한다면 회귀함수의 모수를 추정해 볼 수 있습니다.

위의 회귀 함수에서 회귀 모수는 β1과 β2입니다.

회귀 모수를 추정한 값이 b1과 b2입니다.
관측값 쌍들에 의해 회귀 모수 추정값이 변하므로 b1과 b2는 확률변수입니다.
관측값 쌍들이 모두 정해지면 추정량(공식)을 통해 추정값을 구할 수 있습니다.
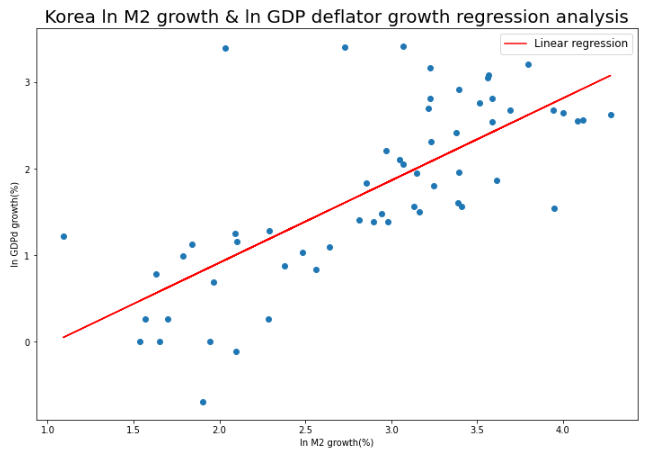
회귀 모수를 추정하는 과정은 각 관측쌍들을 대표하는 회귀선의 y절편과 기울기를 구하는 것과 같습니다.
b1은 x값이 0일 때의 y값, b2는 x값이 한 단위 증가할 때의 y의 평균적인 증가량을 의미합니다.
유의할 점은 x가 0일 때의 관측값이 많지 않다면 b1을 해석하는 것은 유의미하지 않을 수 있다는 것입니다.
다음으로 추정값을 구하기 위한 방법에 대해 알아보도록 하겠습니다.
최소제곱법(OLS: Ordinary Least Squares)
각각의 관측값들의 y값과 회귀선의 수직 거리를 잔차라고 합니다.

위의 관측값들과 회귀선 사이의 노란 선의 길이가 각각의 관측값들의 잔차입니다. (모두 표시하지 않았습니다)
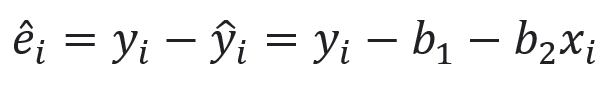
각각의 잔차의 합이 작을수록 회귀선이 모든 관측값들을 대표한다고 할 수 있을 것입니다.
하지만 단순히 각각의 관측값들의 y값에서 회귀선의 y값을 제한 값을 더할 경우 잔차가 양수와 음수가 모두 나오므로 이를 최소화할 수 없습니다.
따라서 각각의 잔차를 제곱하여 모두 더한 값을 최소화하는 방법으로 모수를 추정합니다.
각각의 잔차를 제곱하여 모두 더한 값을 SSE(Sum of Squared Errors)라고 합니다.

SSE를 최소화하는 방법을 사용하여 모수를 추정하는 것을 최소제곱법(OLS)라 합니다.
통계학적으로 SSE를 최소화하는 공식이 존재하며 이를 정규 최소제곱 추정량이라 합니다.

관측값들을 위의 식에 대입하면 단순 선형회귀의 모수를 추정한 추정값을 구할 수 있습니다.
위의 식은 독립변수가 1개인 단순 선형회귀에서만 사용 가능한 공식이며 여러 개의 독립변수를 두고 분석하는 다중회귀분석의 경우 OLS추정량을 구하는 공식이 훨씬 복잡해집니다.
지금까지 회귀 모수를 추정하기 위한 방법 중 최소제곱법(OLS)에 대해 살펴보았습니다.
이번 시간에는 정확히 말하면 회귀 모수의 점 추정량을 구해보았습니다.
다음 시간에는 회귀 모수의 구간 추정량을 구해보겠습니다.
https://bigdata-doctrine.tistory.com/42
회귀 모수 추정: 표준오차(se)를 통한 구간 추정
오늘은 단순 선형회귀의 회귀 모수를 구간추정 하는 방법을 알아보도록 하겠습니다. 구간추정이란 모수가 속할 수 있는 구간을 추정하는 방법입니다. 신뢰도를 통해 모수를 가질 수 있는 특정
bigdata-doctrine.tistory.com
'정보 > 수리통계' 카테고리의 다른 글
| 회귀 모수에 대한 검정: 유의성검정과 p-값 (0) | 2023.08.22 |
|---|---|
| 회귀 모수에 대한 검정: 가설검정 (0) | 2023.07.29 |
| 회귀 모수 추정: 표준오차(se)를 통한 구간 추정 (2) | 2023.07.25 |
| 단순 선형회귀 모형에 관한 가정 (SR3~SR6) (0) | 2023.03.13 |
| 단순 선형회귀 모형에 관한 가정 (SR1~SR2) (0) | 2023.03.06 |

